One difficulty with GPU hardware tessellation is the complexity of programming it. Tessellation offers a number of modes and options; it’s hard to remember which things do what, and how all the pieces fit together. I use tessellation just infrequently enough that I’ve always completely forgotten this stuff since the last time I used it, and I’m getting sick of looking it up and/or figuring it out by trial and error every time. So here’s a quick-reference post for how it all works!

This article is written from a D3D perspective and will mostly use D3D terminology. However, the same hardware functionality is exposed in OpenGL in essentially the same way, as ARB_tessellation_shader, which is in core in OpenGL 4.0+.

Tessellation Refresher

When tessellation is enabled, the GPU pipeline gains two(ish) additional stages:

• Hull shader—per-patch shader. Runs right after vertex shading, and can see the data for all the vertices in the patch. Primarily responsible for setting tessellation factors, though it can also modify the vertex data if you want. Also useful for per-patch frustum culling.

• Domain shader—post-tessellation vertex shader. Gets the UV coordinates of the generated vertex within the patch, and is responsible for interpolating, displacing, and what-have-you to produce the final vertex data to rasterize.

The “patch-constant” part of the hull shader looks sort of like an extra stage of its own in D3D; it has a separate entry point from the main hull shader, and it conceptually runs at a lower frequency (per-patch rather than per-patch-vertex). In OpenGL, though, it’s all tossed together in one entry point for the compiler to sort out.

What constitutes a “patch” on the input side is pretty free-form. A patch can have any number of vertices you want, from 1 to 32, and the meaning of those vertices is up to the interpretation of the hull and domain shaders. Common patch sizes include: 3 for triangular patches (e.g. using Phong tessellation), 4 for quad patches, or 16 for bicubic patches with all the control points.

Warning: Conventions Ahead

Note that because the meaning of the vertices is up to the interpretation of the hull and domain shaders, there is no canonical vertex order for patches! Different conventions for vertex order are possible, which can lead to different people’s or projects’ tessellation shaders having different mappings between vertex index and the patch UVs and tess factors.

The thing that isn’t up to individual convention, but is fixed by the hardware and API definitions, is the relationship between patch UVs and tess factors. Those relationships are shown in the diagrams below, and carry through regardless of which conventions you’re using, or which API.

Domains

The “domain” mode controls the shape of the tessellated mesh that will be generated and fed through the domain shader. There are three domains supported by the hardware: triangle, quad, and isoline.

Triangle

The triangle domain generates triangular output patches. It has three edge tess factors, which specify the number of segments that each edge of the triangle gets subdivided into. It has a single “inside” tess factor, which specifies the number of mesh segments from each edge to the opposite vertex. The domain shader receives three barycentric coordinates, which always sum to 1. The barycentrics are represented by colors (UVW = RGB) in the diagram below.

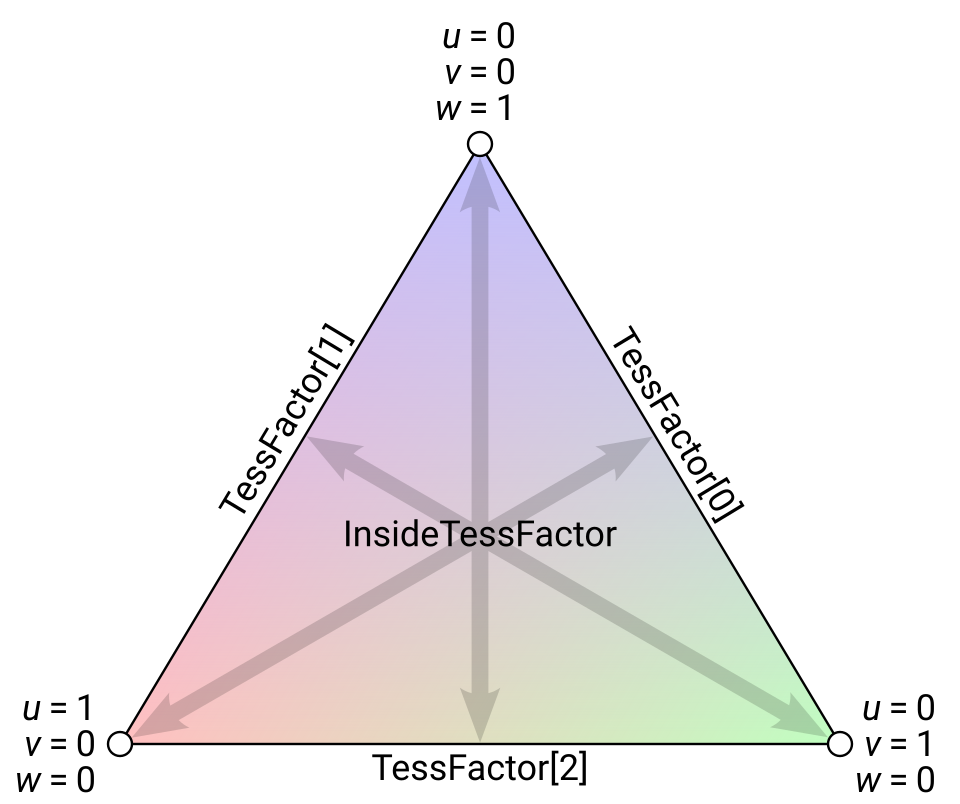
Here’s an HLSL snippet for a basic triangle domain shader that just interpolates positions:

[domain("tri")]
void ds(
    in float edgeFactors[3] : SV_TessFactor,
    in float insideFactor : SV_InsideTessFactor,
    in OutputPatch<VData, 3> inp,
    in float3 uvw : SV_DomainLocation,
    out float4 o_pos : SV_Position)
{
    o_pos = inp[0].pos * uvw.x + inp[1].pos * uvw.y + inp[2].pos * uvw.z;
}

Note that here I’ve used the convention that each component of the UVW vector is the weight for the same-index vertex (the first component goes with the first vertex, etc). This leads to each edge tess factor controlling the edge opposite the same-index vertex.

Another reasonable convention would be that vertex 0 lies at the origin of UV space (i.e. at u = 0, v = 0, w = 1), vertex 1 lies along the U axis, and vertex 2 lies along the V axis. This would lead to a different expression in the domain shader, and a different mapping between vertices and edge tess factors, but the diagram above wouldn’t change.

In a real-world case, you’d probably have additional vertex attributes being interpolated similarly. Higher-order interpolation and displacement mapping could also be applied.

Quad

The quad domain generates quadrilateral output patches; it has four edge tess factors, and two inside factors, which control the number of segments between pairs of opposite edges. The domain shader receives two-dimensional UV coordinates, represented as red and green in the diagram below.

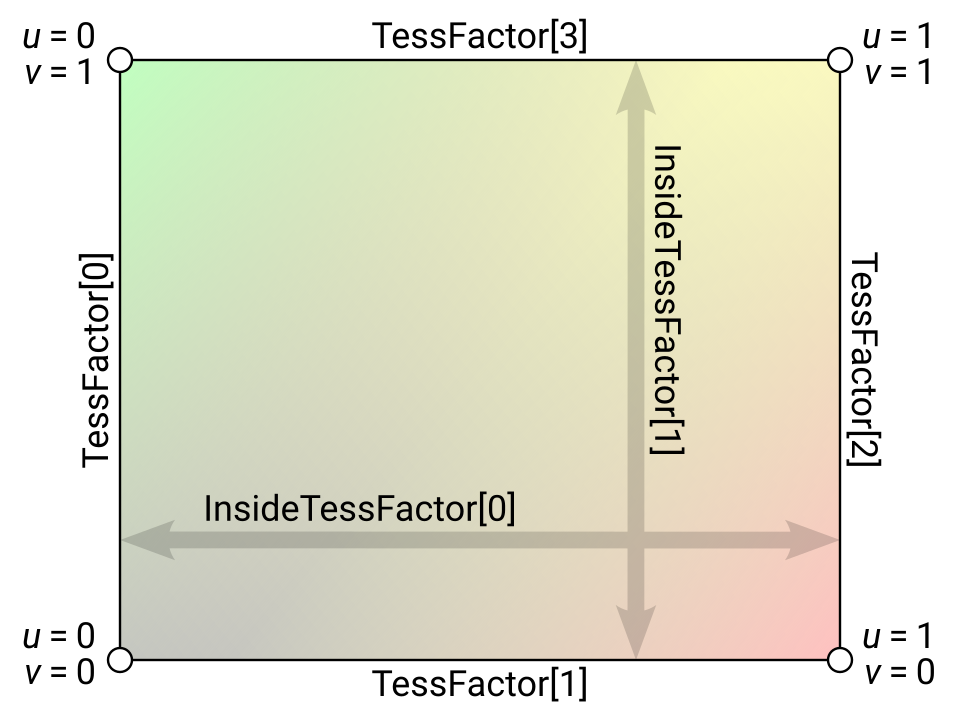
HLSL for a basic quad domain shader:

[domain("quad")]
void ds(
    in float edgeFactors[4] : SV_TessFactor,
    in float insideFactors[2] : SV_InsideTessFactor,
    in OutputPatch<VData, 4> inp,
    in float2 uv : SV_DomainLocation,
    out float4 o_pos : SV_Position)
{
    o_pos = lerp(lerp(inp[0].pos, inp[1].pos, uv.x),
                 lerp(inp[2].pos, inp[3].pos, uv.x),
                 uv.y);
}

As we saw in the triangle case, there are multiple possible vertex order conventions. I’ve chosen to put the vertices in triangle-strip order: bottom-left, bottom-right, top-left, top-right. This is the order that you’d submit the vertices to draw a quad as a two-triangle strip. Another reasonable convention would be counterclockwise order around the quad, which would swap vertices 2 and 3 relative to mine.

Isoline

The isoline domain is an odder and less-used one. Instead of producing triangles, it produces a set of line strips. The line strips come in a quadrilateral shape, same as the quad domain, but they’re subdivided along the U axis and discretely spaced along the V axis. The isoline domain has only two edge tess factors (defined the same way as for the quad domain), and no inside factors.

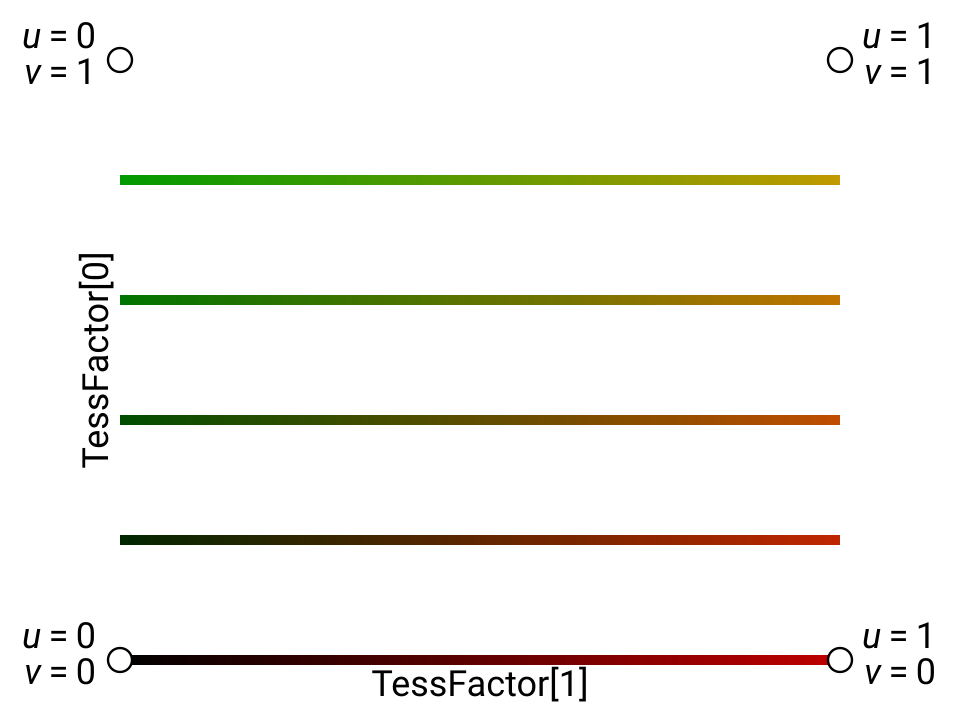
Note that the “last” line strip, that would appear at v = 1, is missing; this is so neighboring isoline patches don’t produce overlapping line strips along their shared edge.

HLSL for a basic isoline domain shader (note that the body is the same as for the quad domain, above—the only difference is the number of tess factors):

[domain("isoline")]
void ds(
    in float factors[2] : SV_TessFactor,
    in OutputPatch<VData, 4> inp,
    in float2 uv : SV_DomainLocation,
    out float4 o_pos : SV_Position)
{
    o_pos = lerp(lerp(inp[0].pos, inp[1].pos, uv.x),
                 lerp(inp[2].pos, inp[3].pos, uv.x),
                 uv.y);
}

Spacing (aka Partitioning) Modes

Spacing modes (actually called “partitioning” modes in D3D, but I like the OpenGL term better) affect the interpretation of the tessellation factors. Broadly speaking, the tess factors are just the number of segments that a given edge or UV axis will be subdivided into, but there are three choices for the detailed behavior.

(There’s also a fourth mode, “pow2”, but I’ll ignore it here, since it’s just integer mode with an extra restriction. It also doesn’t exist in OpenGL.)

Integer Spacing

In integer spacing, also called equal spacing, fractional tess factors are rounded up to the nearest integer. The useful range is [1, 64]. There are no smooth transitions; subdivisions are always equally spaced in UV distance, and we just discretely pop from one to the next.

Here’s a video showing the tess factors animating from 1 to 64 in integer spacing mode, using the triangle, quad, and isoline domains respectively. (For the isoline case, I also rendered a dot at each vertex so you can see where they are along the lines.)

Fractional-Odd Spacing

The fractional spacing modes provide smooth transitions between different subdivision levels, by morphing vertices around so that edges smoothly expand or collapse as the tess factors go up and down.

In the case of fractional-odd mode, the number of segments is defined by rounding the tess factors up to the nearest odd integer, and the blend factor for vertex morphing is defined by how far you had to round. This mode matches integer spacing when you’re exactly on an odd integer. The useful range is [1, 63].

Here’s a video:

Note that in isoline mode, the V axis (between the lines) always uses integer spacing behavior. Only the U axis (along the lines) gets fractional spacing.

Fractional-Even Spacing

Fractional-even spacing is the same as fractional-odd, but using even integers instead. The useful range is [2, 64]. Note that the “identity” tess factor of 1 is not available in this mode! Everything always gets tessellated by at least a factor of 2.

Video:

Why is there no “fractional-integer” mode?

You might be wondering why fractional spacing only comes in “odd” and “even” flavors. Why don’t we have a fractional mode that interpolates between all integer tess factors?

The answer lies with the symmetry of the tessellation patterns. The patterns are chosen to be (as nearly as possible) invariant under flips and rotations of the UV space. For example, in the triangle domain, the output mesh looks the same if you rotate the triangle by 120° either direction, or reflect it across the line between a vertex and the midpoint of the opposite edge. Similarly, quad-domain meshes are unchanged by a rotation by 90° or a reflection along either the U or V axis. The only place the symmetry breaks is the very middle row of quads, when a rounded tess factor is odd; then, that row’s diagonals have to go one way or the other, so they can’t be symmetric.

If this symmetry is going to be maintained, then the tess factors can only change in increments of two. Anytime you add a subdivision at one place along an edge or UV axis, you must also add another subdivision at the corresponding place reflected across the midpoint of that edge or axis. Otherwise, you’ll break the symmetry. Thus, your rounded tess factors must be either all odd or all even integers.

This raises the further question: why do we have these symmetry requirements at all? Well, along the edges of a patch, the reflection symmetry is critical to prevent cracking between patches! Two adjacent patches will construct their shared edge with opposite vertex orders, so the vertices generated when tessellating that edge must be invariant under interchanging the endpoints.

For the interior of the patch, the symmetry seems less critical, but I suppose that maintaining the same symmetry makes it simpler to generate triangles connecting the interior vertices to the edge vertices. It also supports the earlier-mentioned idea that there’s no canonical vertex order for patches: different vertex order conventions may effectively rotate or flip the UV space, but if it’s all symmetric, that doesn’t matter.

Further Reading

• Tessellation in Call of Duty: Ghosts by Wade Brainerd (GDC 2014) shows how to use tessellation to implement Catmull-Clark subdivision surfaces.
• Tessellation chapter from Fabian Giesen’s “A trip through the Graphics Pipeline” series discusses some finer points of the generated mesh topologies and how the shaders execute on the GPU.
• My Tessellation Has Cracks! by Bryan Dudash addresses the annoyingly subtle problem of ensuring that your domain shader doesn’t introduce cracks between adjacent patches.
• SIGGRAPH 2010 course on hair rendering by Cem Yuksel and Sarah Tariq uses isoline tessellation to increase the density of rendered hairs (see Chapter 2 at the link).
• OpenGL extension spec for tessellation.

Tessellation is one of those GPU features that doesn’t seem to get much love. It presents many challenges—authoring issues and performance, as well as the engineering complexity of using it. Hopefully, some better documentation will help with the last.